In systems, where multiple robots operate in a shared area, one has to ensure that the robots do not collide not only with known static and dynamic obstacles, but also with each other. Such a task can be accomplished in the framework of multi-robot path planning by planning coordinated trajectories for the whole multi-robot team. However, the problem of finding coordinated trajectories is known to be NP-hard even for the simplest models of robots.

The known complete approaches suffer from computational complexity that is exponential in the number of robots. In our work we characterize a class of environments called well-formed infrastructures, where solution can be computed using a decoupled approach efficiently (in polynomial time in the number of robots) in a guaranteed manner.

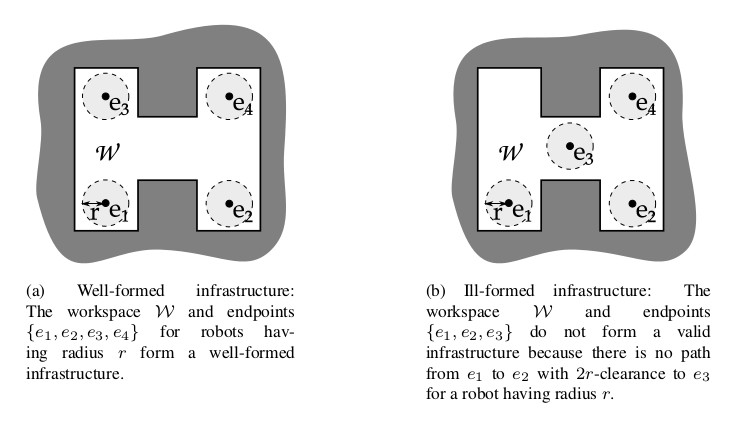
Well-formed Infrastructures

To model systems such as warehouses, factories, rail roads, road networks etc., we introduce the notion of an infrastructure. An infrastructure is a pair (W, E), where W is a workspace (described by a set of obstacle-free coordinates) and a set of points E ⊂ W represents distinguished locations in the environment called endpoints (modeling e.g. storage locations in a warehouse, workplaces in a factory, parking places, road stops, etc.). Vehicles operating in such an infrastructure are assumed to only move between the endpoints of the infrastructure. A well-formed infrastructure has its endpoints distributed in such a way that any robot standing on an endpoint cannot completely prevent other robots from moving between any other two endpoints. In a well-formed infrastructure, a robot is always able to find a collision-free trajectory to any other unoccupied endpoint by waiting for other robots to reach their destination endpoint, and then by following a path around the occupied endpoints, which is in a well-formed infrastructure guaranteed to exist.

Revised Prioritized Planning (RPP) and its Asynchronous Decentralized Variant (ADPP)

In the paper

• M. Čáp, P. Novák, A. Kleiner, and M. Selecký, “Prioritized planning algorithms for trajectory coordination of multiple mobile robots,” IEEE transactions on automation science and engineering, vol. 12, iss. 3, p. 835–849, 2015.
  [Bibtex]

  @article{cap_2015_b,
  author = {Michal \v{C}\'{a}p and
  Peter Nov{\'{a}}k and
  Alexander Kleiner and
  Martin Seleck{\'{y}}},
  title = {Prioritized Planning Algorithms for Trajectory Coordination of Multiple Mobile Robots},
  journal = {{IEEE} Transactions on Automation Science and Engineering},
  volume = {12},
  number = {3},
  pages = {835--849},
  year = {2015},
  url = {http://dx.doi.org/10.1109/TASE.2015.2445780},
  doi = {10.1109/TASE.2015.2445780},
  webpage = {http://michalcap.net/decoupled-methods-for-multi-robot-motion-planning/},
  video = {https://www.youtube.com/watch?v=dFm-JJhyuv0},
  codebase = {https://github.com/mcapino/adpp-journal},
  }

we show that a slightly adapted version of classical prioritized planning approach, where robots plan sequentially one after each other such that robots that plan later avoid collisions with robots that planned earlier is guaranteed to solve all trajectory coordination queries of robots that move between two endpoints of a well-formed infrastructure.

The principle can be also generalized to asynchronous decentralized systems, where the trajectories are not planned centrally for all the robots, but rather each robots uses its own on-board computer to compute its trajectory. Such an approach is not only beneficial in terms of speed of the computation, but it also more naturally applicable to heteregenous multi-robot systems, because the robots do not need to formalize and communicate their objectives and motion constraints to a central solver.

In the following video, we show an illustration of both algorithms coordinating simulated multi-robot team on three real-world maps:

 

Real-world Deployment

We have deployed the asynchronous decentralized version of prioritized planning as a mechanism for coordination in real-world multi-robot systems. The first video shows deployment in a multi-UAV system, while the second video shows deployment of the technique for coordination in a automated mobility-on-demand system.

Source code

The implementation of the presented algorithms and the benchmark insances used to generate the results in the paper can be downloaded through Github at https://github.com/mcapino/adpp-journal.

---

COBRA: Continuous Best-Response Approach

In this paper

• M. Čáp, J. Vokřínek, and A. Kleiner, “Complete decentralized method for on-line multi-robot trajectory planning in well-formed infrastructures,” in Proceedings of the twenty-fifth international conference on automated planning and scheduling, ICAPS 2015, jerusalem, israel, june 7-11, 2015., 2015, p. 324–332.
  [Bibtex]

  @inproceedings{cap_2015_a,
  author = {Michal \v{C}\'{a}p and
  Ji\v{r}\'{i} Vok\v{r}\'{i}nek and
  Alexander Kleiner},
  title = {Complete Decentralized Method for On-Line Multi-Robot Trajectory Planning in Well-formed Infrastructures},
  booktitle = {Proceedings of the Twenty-Fifth International Conference on Automated
  Planning and Scheduling, {ICAPS} 2015, Jerusalem, Israel, June 7-11,
  2015.},
  pages = {324--332},
  year = {2015},
  webpage = {http://michalcap.net/decoupled-methods-for-multi-robot-motion-planning/},
  video = {https://www.youtube.com/watch?v=KUSPCOmX1ig},
  codebase = {https://github.com/mcapino/cobra-icaps2015},
  slides = {http://michalcap.net/wp-content/papercite-data/pdf/cap_2015_a-slides.pdf},
  }

we extend the prioritized planning approach to systems where the robots are not coordinated in batch, but rather incrementally during each task assignment. To see when can be such an algorithm useful, consider a factory where the intermediate products are moved between the individual workstations by automated transport robots. A worker in such a factory can call a robot to its workstation, puts an item to a basket mounted on the robot and orders the robot to relocate to another workstation. To successfully fulfill the task, the robot has to coordinate its motion with other transport robots operating in the factory. Even though the coordinated trajectories can be found using a batch multi-robot trajectory planner from the current positions the robots and their destinations, the other robots may be at the moment of planning outside of an endpoint and thus RPP or AD-RPP cannot guarantee the ability to find a solution. Thus, we introduce an algorithm called Continuous Best Response Approach (COBRA) that achieves guaranteed performance even if the tasks are assigned to robots incrementally.

The following video shows COBRA in action:

Source code

The implementation of the algorithm and the benchmark instances used to generate the results in the paper can be downloaded through Github at https://github.com/mcapino/cobra-icaps2015.